Wie Viele Dreiecke Gibt Es In Einem Pentagramm

Pentagramm,
Schläfli-Symbol {5/2}, {v/3}.

Pentagramm (von altgriechisch πέντε pénte „fünf" und γραμμή grammē „Linie, Strich"; πεντάγραμμος pentágrammos „mit fünf Linien") bezeichnet eine Grade des fünfzackigen Sterns, auch Fünfstern genannt, die sich ergibt, wenn beim Verbinden der fünf Eckpunkte jedes Mal einer bzw. zwei übersprungen werden und die somit erzeugten Sehnen gleich lang sind. Notiert wird dieser regelmäßige Stern mit dem Schläfli-Symbol ${\displaystyle \left\{5/2\right\}}$ bzw. ${\displaystyle \left\{5/three\right\}}$ . Verbreitet sind auch die Bezeichnungen Drudenfuß bzw. Drudenstern, Pentakel sowie Pentalpha, da es sich durch fünf ineinander stehende Alphas („Α") bilden lässt. Da das Pentagramm fünf Spitzen lid, gibt es zwei grundsätzliche Arten seiner Ausrichtung: mit einer Spitze nach oben (dann zeigen zwei Spitzen nach unten und zwei zur Seite), oder mit einer Spitze nach unten (dann zeigen zwei Spitzen nach oben und zwei zur Seite). Letzteres wird auch als „umgekehrtes" oder „invertiertes" Pentagramm bezeichnet.

Unicode [Bearbeiten | Quelltext bearbeiten]

Das Pentagramm ist im Unicodeblock Verschiedene Symbole aufgenommen. Am Codepunkt U+26E4 (9956) ⛤ unter dem Namen „PENTAGRAM" und am Codepunkt U+26E7 (9959) ⛧ als „INVERTED PENTAGRAM".

Geometrie [Bearbeiten | Quelltext bearbeiten]

Konstruktion [Bearbeiten | Quelltext bearbeiten]

Die Punkte A, B, C, D, Eastward definieren ein regelmäßiges Fünfeck (rot) und ein Pentagramm (violett)

Aus fünf gleichmäßig, also in Abständen von 72°, auf einem Kreis verteilten Punkten lassen sich mittels Sehnen zwei fünfachsig symmetrische Figuren erstellen:

• Die fünf Sehnen zwischen benachbarten Punkten bilden ein regelmäßiges Fünfeck mit Winkeln von jeweils 108°.
• Dice fünf Sehnen zwischen nicht benachbarten Punkten bilden zusammen das Pentagramm mit spitzen Winkeln von 36°.

Geometrische Eigenschaften [Bearbeiten | Quelltext bearbeiten]

Die inneren Abschnitte der Sehnen des Pentagramms bilden wiederum ein regelmäßiges Fünfeck. Gegenüber dem äußeren ist es um 36° gedreht. Die Zacken des Pentagramms sind gleichschenklige Dreiecke. Dice Winkel zwischen Basis und Schenkeln dieser Dreiecke betragen 72°.

Das innere Fünfeck bildet zusammen mit je zwei nicht benachbarten Zacken ein gleichschenkliges Dreieck mit stumpfer Spitze, dem schon erwähnten 108°-Winkel.

Zeichnet human in das innere Fünfeck wieder ein Pentagramm, then bilden dessen Sehnen mit Teilen der Sehnen des äußeren Pentagramms ebenfalls gleichschenklige Dreiecke mit stumpfer Spitze von 108°. Deren Mittelsenkrechten liegen parallel zu denen der Zackendreiecke, die ihrerseits die Symmetrieachsen aller Pentagramme und Fünfecke bilden.

Äußeres Fünfeck, Pentagramm und inneres Fünfeck haben denselben Mittelpunkt. Jede Sehne des inneren Pentagramms verläuft parallel zu einer jenseits des Mittelpunktes gelegenen Sehne des äußeren Pentagramms.

Alle Winkel zwischen den Kanten des Pentagramms und des umschließenden Fünfecks betragen besides 36°, 72° oder 108°. Die fünf Symmetrieachsen haben zu den Kanten Winkel von eighteen°, 54° und xc°.

Goldener Schnitt [Bearbeiten | Quelltext bearbeiten]

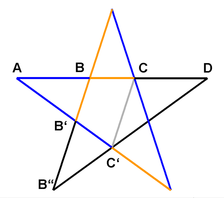
Alle Sehnen und durch Schnittpunkte begrenzte Sehnenteile eines Pentagramms samt äußerem und innerem Fünfeck haben nur vier verschiedene Längen. Davon stehen jeweils aufeinander folgende zueinander im Verhältnis des Goldenen Schnitts, d. h. die folgenden Längenverhältnisse sind gleich:

${\displaystyle {\frac {AB}{BC}}={\frac {AC}{AB}}={\frac {AD}{Air conditioning}}}$

Denn es gilt z. B. für das erste Verhältnis:

${\displaystyle CC'=CD}$

Das Dreieck ${\displaystyle CC'D}$ ist gleichschenklig, da es eine proportionale Verkleinerung des gleichschenkligen Dreiecks ${\displaystyle BB''D}$ ist, denn die Innenwinkel der beiden Dreiecke sind gleich.

${\displaystyle AB=CD}$ und ${\displaystyle BB'=BC}$

Aufgrund des Strahlensatzes gold:

${\displaystyle {\frac {AB}{BB'}}={\frac {Air-conditioning}{CC'}}}$

Betrachten wir das Verhältnis

${\displaystyle \Phi ={\frac {AB}{BC}}={\frac {AC}{AB}}={\frac {AB+BC}{AB}}}$ ,

dann ist ${\displaystyle \Phi =1+{\frac {1}{\Phi }}}$ und entspricht somit der Definition des Goldenen Schnitts, somit gilt ${\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}=1{,}618...}$ .

Formeln [Bearbeiten | Quelltext bearbeiten]

Mathematische Formeln zum Pentagramm

Flächeninhalt	${\displaystyle A={\frac {i}{four}}\cdot {\sqrt {250+110\cdot {\sqrt {five}}}}\cdot southward^{2}\approx 5{,}568\cdot s^{2}}$
	${\displaystyle A={\frac {1}{ii}}\cdot {\sqrt {25-10\cdot {\sqrt {five}}}}\cdot a^{2}\approx 0{,}812\cdot a^{ii}}$
Umfang	${\displaystyle U=5\cdot l={\frac {5+5\cdot {\sqrt {5}}}{2}}\cdot a=(10+five\cdot {\sqrt {five}})\cdot south}$
Länge der Sehne	${\displaystyle l=\Phi \cdot a={\frac {1+{\sqrt {5}}}{2}}\cdot a\approx one{,}618\cdot a}$
	${\displaystyle fifty=\Phi ^{three}\cdot due south=(2+{\sqrt {5}})\cdot s\approx 4{,}236\cdot s}$
	${\displaystyle l={\frac {ane}{2}}\cdot {\sqrt {10+2\cdot {\sqrt {5}}}}\cdot r\approx 1{,}902\cdot r}$
Seitenlänge des inneren Fünfecks	${\displaystyle s={\frac {a}{\Phi ^{ii}}}={\frac {3-{\sqrt {5}}}{2}}\cdot a\approx 0{,}382\cdot a}$
	${\displaystyle s={\frac {l}{\Phi ^{iii}}}=({\sqrt {v}}-2)\cdot 50\approx 0{,}236\cdot l}$
	${\displaystyle s={\frac {1}{2}}\cdot {\sqrt {50-22\cdot {\sqrt {5}}}}\cdot r\approx 0{,}449\cdot r}$
Seitenlänge des äußeren Fünfecks	${\displaystyle a=(\Phi +1)\cdot s=\Phi ^{ii}\cdot s={\frac {3+{\sqrt {5}}}{2}}\cdot s\approx 2{,}618\cdot due south}$
	${\displaystyle a=(\Phi -1)\cdot l={\frac {l}{\Phi }}={\frac {{\sqrt {5}}-1}{2}}\cdot l\approx 0{,}618\cdot l}$
	${\displaystyle a={\frac {i}{2}}\cdot {\sqrt {x-ii\cdot {\sqrt {5}}}}\cdot r\approx 1{,}176\cdot r}$
Umkreisradius	${\displaystyle r={\frac {1}{10}}\cdot {\sqrt {50-10\cdot {\sqrt {5}}}}\cdot l\approx 0{,}526\cdot l}$
	${\displaystyle r={\frac {1}{10}}\cdot {\sqrt {l+10\cdot {\sqrt {five}}}}\cdot a\approx 0{,}851\cdot a}$
	${\displaystyle r={\frac {1}{10}}\cdot {\sqrt {250+110\cdot {\sqrt {5}}}}\cdot s\approx 2{,}227\cdot south}$

Polyeder mit Pentagrammen [Bearbeiten | Quelltext bearbeiten]

Einige Polyeder haben Pentagramme als Seitenflächen, zum Beispiel der Dodekaederstern und der Ikosaederstern. Diese zwei Polyeder sind Kepler-Poinsot-Körper.

• 

• 

Flora [Bearbeiten | Quelltext bearbeiten]

Das Fünfeck taucht in verschiedenen Zusammenhängen in der Natur auf, so ist es ein Kennzeichen der Gewöhnlichen Stockrose.

Geschichte und kulturelle Bedeutung [Bearbeiten | Quelltext bearbeiten]

Antike [Bearbeiten | Quelltext bearbeiten]

Das Pentagramm wurde auf einem Krug aus der mesopotamischen Djemdet-Nasr-Zeit, d. h. um 3000 five. Chr., gefunden, und wird als Symbol für „Gottheit" gedeutet.^[one]

Pythagoras kannte es als Symbol für Gesundheit. Ihn interessierte daran besonders der mathematische Aspekt des Goldenen Schnitts. Da homo es in einem Zug zeichnen kann und am Schluss wieder zum Anfang gelangt, galt es auch als Zeichen für den Kreislauf des Lebens. Abraxas, Gott der Gnostiker, wurde ebenfalls durch ein Pentagramm symbolisiert, weil er fünf Urkräfte in sich vereint.

Heraldik [Bearbeiten | Quelltext bearbeiten]

Auch in der Heraldik, also auf Wappen, und bei Flaggen, wird der Drudenfuß als gemeine Figur verwendet. Marokko und Äthiopien führen einen Drudenfuß in den Flaggen, Kommunen wie Knielingen, Giebenach und Schlotheim in ihren Wappen.

Im Sakralbau [Bearbeiten | Quelltext bearbeiten]

Kirche St. Peter und Paul in Kaarma (13. Jahrhundert)

Das Pentagramm mit seinem Goldenen Schnitt prägte manchen Kirchenbau. Pentagramme sind noch heute an vielen Fensterrosetten gotischer Kirchengebäude zu sehen. An der Ostseite des Turms der Marktkirche Hannover ist ebenfalls ein Drudenfuß zu sehen. Eine christliche Deutung für die fünf Ecken sind die fünf Wunden Jesu Christi.

Freimaurer-Symbol [Bearbeiten | Quelltext bearbeiten]

Von den Dombauhütten kam das Pentagramm zu den Freimaurern und wurde das übergeordnete Symbol auf ihren Arbeitsteppichen. Seine fünf Spitzen weisen auf die Tugenden der Klugheit, der Gerechtigkeit, der Stärke, der Mäßigung und des Fleißes hin.^[2]

Weitere symbolische Deutungen der fünf Ecken des Pentagramms sind der Geist und dice vier Elemente Feuer, Wasser, Erde und Luft; oder auch Äther und die vier Himmelsrichtungen Norden, Süden, Westen und Osten.

Der Flammende Stern ist ein freimaurerisches Pentagramm, das von einer Gloriole umgeben ist und zentral den Buchstaben G enthält (identische Bedeutung).

Numismatik [Bearbeiten | Quelltext bearbeiten]

Als Symbol auf Münzen ist das Pentagramm bereits seit dem Frühmittelalter auf merowingischen Münzen nachweisbar. Auch auf den Münzen und Geldscheinen Französisch-Marokkos ist es vielfach zu finden. Beispiele:

• 

  Tanger, 0,50 Francs, Datum unbekannt

• 

  10 Francs, 1943

• 

  fifty Centimes, 1945

• 

  1 Franc, Datum unbekannt

Pentakel [Bearbeiten | Quelltext bearbeiten]

Das Pentagramm, insbesondere wenn es von einem Kreis umschlossen ist, wird auch als Symbol für Amulette verwendet und Pentakel genannt. Das Wort kann aber auch allgemein Amulette zur magischen Beschwörung bezeichnen, auch wenn ein anderes Symbol darauf ist.

Religion und Okkultismus [Bearbeiten | Quelltext bearbeiten]

Drudenfuß als Schutzsymbol an einem Haus in Ahrweiler von 1639

In mittelalterlicher und nachmittelalterlicher Zeit galt das Pentagramm als Bannzeichen gegen das Böse sowie als Zauber- und Abwehrzeichen gegen Dämonen. Der Proper name Drudenfuß wird zum einen damit erklärt, dass das Zeichen als Schutzzeichen gegen nächtliche Spukgeister, die Druden, angesehen wurde. Es gab aber auch den Glauben, dass Druden selbst einen vogelartigen Fußabdruck hinterlassen, der in etwa dem Pentagramm gleicht.

In Goethes Faust I (Vers 1395 f.) hindert das Zeichen den Teufel Mephistopheles daran, Fausts Studierzimmer zu verlassen:

Mephistopheles: „Gesteh' ich's nur! daß ich hinausspaziere / Verbietet mir ein kleines Hinderniß, / Der Drudenfuß auf eurer Schwelle –"

Faust: „Das Pentagramma macht dir Pein?"

Das Pentagramme de Faust aus Éliphas Lévis Dogme et rituel de la haute magie

Seit dem französischen Okkultisten Éliphas Lévi wird insbesondere das „umgekehrte" Pentagramm/Pentakel mit Okkultismus und Satanismus in Verbindung gebracht. In Lévis Dogme et rituel de la haute magie aus der Mitte des 19. Jahrhunderts wird es als „Zeichen der Ziege des Sabbaths" bezeichnet, wobei dice Zacken jeweils für die Hörner, dice Ohren und den Bart der Ziege stehen. Umgekehrt wurde das auf zwei Spitzen stehende Pentagramm mit Jesus Christus identifiziert, wobei Jesu eigentlicher Name יְהוֹשׁוּעַ (Jehoschua) beziehungsweise יֵשׁוּעַ (Jeschua) vom Tetragrammaton יהוה (JHWH) ausgehend mit יהשוה (Jahschuah) wiedergegeben und als Pentagrammaton bezeichnet wurde.^{[3] [iv]}

Darauf bauten zahlreiche spätere Okkultisten auf. Mit einem Ziegenkopf in einem von verzerrten hebräischen Zeichen (LVYThN לִוְיָתָן) umringten invertierten Pentagramm erschien es 1961 auf dem Cover von Maurice Bessys Histoire en yard Images de la Magie; Anton Szandor LaVey übernahm dieses unter der Bezeichnung Sigil of Baphomet als Zeichen seiner 1966 gegründeten Church building of Satan. LaVey benutzte das Siegel des Baphomet auch für die Cover der Schallplatte The Satanic Mass (1968) und der Satanischen Bibel (1969).

In den 1980er Jahren wurde das invertierte Pentagramm in der Metal-Szene, insbesondere im Blackness- und Death Metal, als Symbol für das Böse oder den Satanismus beliebt, das Siegel des Baphomet erschien z. B. auf Schallplatten wie Jamras The 2d Coming (1972) und Venoms Welcome to Hell (1982). Ferner gibt es eine Doom-Metal-Ring namens Pentagram. Das Pentakel (Pentagramm mit Kreis) ist auch im Neuheidentum, insbesondere in der neureligiösen Bewegung Wicca, ein wichtiges Symbol. In dem Horrorfilm Pentagram des Regisseurs Steve Lawson von 2019 beschwören vier Jugendliche, dice durch schwarze Magie in einem Pentagramm auf dem Dachboden eines verlassenen Hauses gefangen sind, den Dämon Asmodäus.

Siehe auch [Bearbeiten | Quelltext bearbeiten]

• Hexagramm, Davidstern, „Siegel Salomos"
• Sigillum Dei
• Heptagramm

Literatur [Bearbeiten | Quelltext bearbeiten]

• Gerd Becker: Das Pentagramm – Symbol in Marokko. Religion, Politik und Magie im maghrebinischen Königreich. Wayasbah, Hamburg 1989, ISBN 978-three-925682-xiii-i.

Weblinks [Bearbeiten | Quelltext bearbeiten]

• Pentagram. Wolfram Research

Einzelnachweise [Bearbeiten | Quelltext bearbeiten]

1. ↑ V. Gordon Childe: New Lite on the almost ancient East. 1928 (1958), Southward. 134 + Abbildung Plate XXI; annal.org.
2. ↑ Georg Schuster: Geheime Gesellschaften, Verbindungen und Orden. fourier (Nachdruck etwa 1992), B. 2, Due south. 113.
3. ↑ The Pentagram as Pentagrammaton. Byzant Mystical, abgerufen am 25. Juli 2012 (englisch).
4. ↑ Paula Findlen: Athanasius Kircher: The Last Human being Who Knew Everything. Routledge, New York City/London 2004, ISBN 0-415-94015-X, Southward.154 (eingeschränkte Vorschau in der Google-Buchsuche).

Source: https://de.wikipedia.org/wiki/Pentagramm

Share this post